The Q factor indicates the performance of a coil capacitor inductor in terms of its losses and bandwidth. The higher the value of the Quality factor is a desired feature for a tuned circuit. The higher the Q factor, the narrower the bandwidth.
The Q factor is a dimensionless number that describes damping in a circuit and its bandwidth relative to the center frequency.
The resonance in an electrical circuit occurs at a particular frequency, which is called the resonant frequency. AC circuits generally have inductors and capacitors. The reactance of the capacitor and inductor become equal at a specific frequency, and their reactance cancels out. The frequency at which this condition occurs, the circuit is said to be in resonance. Thus, at resonance, all the impedances or admittances cancel each other out, and the circuit behaves like a resistive circuit. The voltage and current of a resonant circuit are in the same phase.
Resonant Frequency of a Circuit
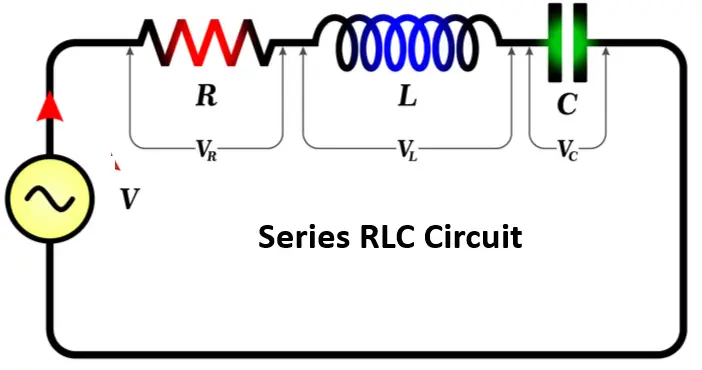
In the case of an RLC circuit, we can find the resonance frequency by equating the inductive and capacitive impedances, which cancel each other out.
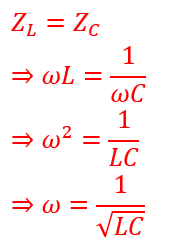
Since,
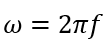
The resonance frequency of the series RLC circuit is;

Q Factor Definition
We know that a coil is known for storing energy when some current passes through it. An ideal coil or a pure inductor would, therefore, cause the current to lag by 90 degrees from the voltage across it. However, in reality, there is no pure inductor, and there is a certain amount of inherent resistance that is available within the coil.
Coils store energy when current passes through them. A pure inductor causes the current to lag 90 degrees from the voltage across it. However, in reality, coils inherently have some resistance, and thus, the current lags by slightly less than 90 degrees from voltage. The coil resistance causes heat loss. It is desired to have lossless coils, but in reality, it is impossible.
The Quality Factor is the ratio of power stored in the coil or reactance to power lost as heat due to coil resistance.
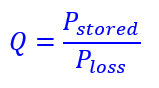
Energy stored in a coil is.
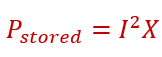
The energy lost in a coil’s resistance is.
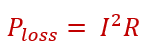
The Quality factor is;

- We can calculate the quality factor of a coil by knowing its reactance and resistance.
- The higher reactance of the coil stores more energy, and its Q factor is better.
- The lower resistance coil has low power loss and a higher quality factor.
Effects of Q factor
A high value of the Q factor is always desirable with RF-tuned circuits. However, in some applications, a defined level of Q may be required. The Q factor affects the following parameters of the tuned circuit.
Bandwidth:
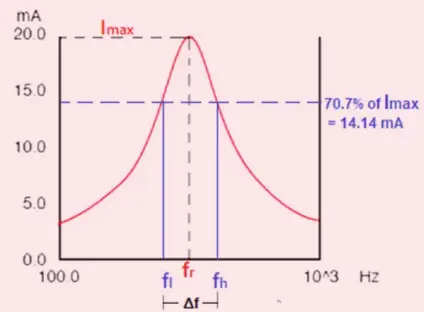
The bandwidth of the tuned circuit filter reduces with an increase in the Quality factor as losses decrease. The high energy storage in an inductor or capacitor causes a tuned circuit to have a sharper bandwidth. It can be observed that with an increase in Q, the 3 dB bandwidth decreases with an increase in quality factor, and thus, the overall response of the tuned circuit improves. A higher degree of selectivity is achieved.
General Spurious Signals:
Tuned circuits and filters can remove spurious signals better with sharper filters and higher Q levels.
Oscillator Phase Noise:
Every oscillator produces phase noise. The phase noise is random fluctuations in the phase of the signal. This results in additional undesirable noise that spreads out from the main carrier. The design of the oscillator is done by keeping the provision of adjusting the quality factor to minimize the phase noise.
Ringing:
As the quality factor of a resonant circuit increases, its losses decrease. This results in a longer decay time for any oscillation within the circuit, causing it to ring more. This is ideal for an oscillator circuit because less energy is lost in the tuned circuit, making it easier to set up and maintain an oscillation.
Q factor formulas
The Q factor formula calculates energy losses within components like inductors and circuits.
The mathematical expression for the Q factor, as defined earlier, is given by the formula below:

When examining the bandwidth of an RF resonant circuit, it is equivalent to calculating the Q factor using the formula:

Quality factor and Damping
A critical aspect of many circuits is damping, determined by the Quality Factor (Q). Q affects the behavior of damped oscillators and other circuits, such as filters. The three main regions considered when referring to the quality factor and damping are as follows.
Under-damped (Q > 1/2) :
When we say that a system is under-damped, its Q factor is higher than 0.5. If the Q factor is only slightly more than 0.5, the system could oscillate once or twice before the oscillation disappears. As the quality factor increases, damping decreases, and oscillations last longer. In an ideal system with an infinite Q factor, oscillation would continue indefinitely without requiring additional stimulus. However, in oscillators, some signal is fed back to provide additional stimulus. A high Q factor typically produces a cleaner signal with lower phase noise levels.
Over-damped (Q < 1/2):
An over-damped system is characterized by a Quality factor that is less than 1/2. In such a system, the losses are high, and there is no overshoot. Instead, the system will exponentially decay and approach the steady state value asymptotically after a step impulse is applied. As the Q factor or quality factor decreases, the system’s response to a step impulse slows down.
Critically damped (Q = 1/2) :
The critically damped system has a Q factor of 0.5, and like an over-damped system, the output does not oscillate and overshoots. Its steady-state output. The system will approach the steady-state asymptote quickly without any overshoot.
In RF resonant systems, a high Q factor is often required. For filters, sufficient selectivity is necessary but not excessive. For oscillators, a high Q factor will result in improved stability and lower phase noise. However, in some systems, the Q factor should not be too high as it may result in filter bandwidths being too narrow, and oscillators may be unable to track over the required range. Generally speaking, the quality factor should be high rather than low.
Read Next: