Definition-Peak Factor is the ratio of the maximum value and the Root Mean Square (RMS) value of an alternating quantity, which can be either voltage or current. The maximum value is also known as the peak value, crest value, or maximum amplitude of the voltage or current. The peak factor is also called the crest factor.
The alternating waveform is time-varying due to its changing magnitude. The highest voltage or current reached by the waveform is expressed as the maximum voltage. Let’s take the example of a sinusoidal waveform to understand the concept.
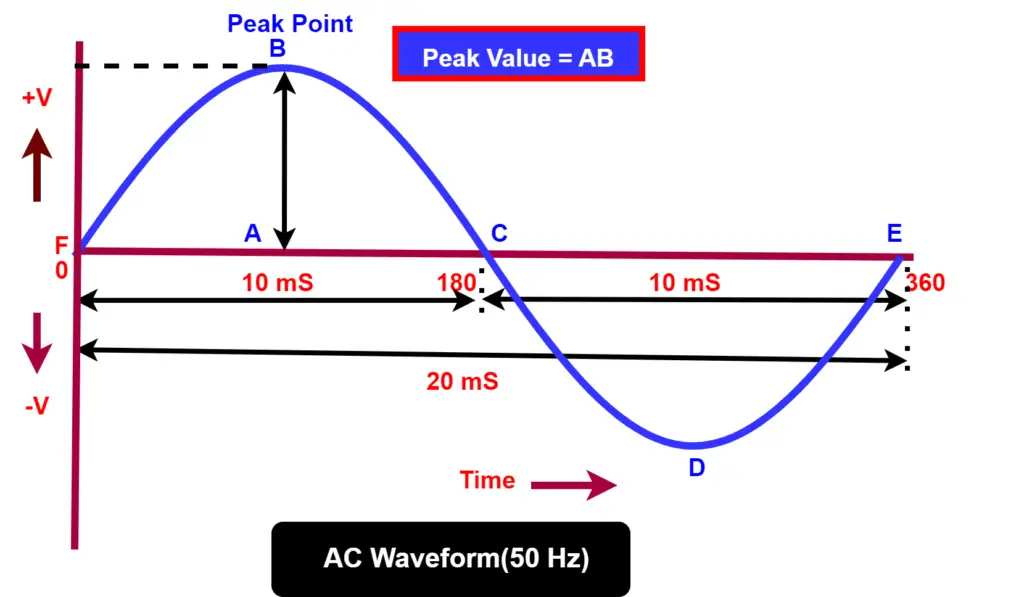
The alternating waveform begins at F, reaches its maximum value at B, and drops to zero at point C. At point C, it changes direction, reaches its maximum negative value at point D, and returns to zero at point E. This cycle repeats continuously in the same manner. The point B is the maximum value point of this waveform.
What is a Peak Factor?
The Peak Factor (PF) shows the relationship between the maximum and the RMS value of the alternating quantity. Here, it is worth understanding what is the RMS value of the alternating voltage or current.
The root mean square value represents the equivalent direct current that produces the same amount of heat in a given time when passed through a resistor. If a resistive circuit produces 100 joules of heat in a specific time with 10 amperes of DC, then the RMS value of AC current will produce the same amount of heat at the same time.

If we supply 24V DC to a heater to produce heat and switch to AC, we need to feed 24V AC (RMS) to the heater to produce the same amount of heat. The RMS value of the AC voltage and current is,
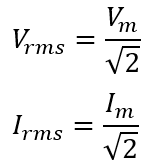
Where Vrms and Irms represent the RMS values of voltage and current, respectively, and Im and Vm are the maximum values of current and voltage.
The crest factor of AC is the ratio of the crest value to the RMS value. Since the maximum value is always greater than the RMS value, the peak factor is always greater than 1.
Peak Factor Formula
The peak factor or crest factor of an alternating quantity is the ratio of its maximum or peak value to its RMS value. It can be mathematically expressed as,
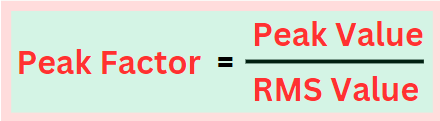
The crest factor for alternating voltage is;

The crest factor for alternating current is;
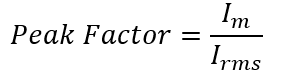
Where Vm and Im are the maximum values of voltage and current, and Vrms and Irms are their respective RMS values.
Peak Factor of Sinusoidal Voltage and Current
The RMS value of sinusoidal AC voltage is;

The ratio of maximum voltage to RMS voltage is the peak factor, so

Putting the value of Vrms from equation 1 into equation 2, we get

The crest factor for sinusoidal AC voltage is 1.414.
Similarly, the peak factor of sinusoidal AC current is,

The peak factor for sinusoidal AC current is 1.414.
Importance of Peak Factor
The peak factor of the system must be studied and analyzed to prevent insulation failure from the higher peak. For instance, a cable designed to operate at 440 volts RMS experiences a voltage stress of 440 x 1.414 = 622 volts. However, if the waveform gets distorted, the PF may change from 1.414, and for instance, if PF changes to 1.6, it means the cable will experience a voltage stress of 440 x 1.6 = 704 volts. This increased voltage can lead to insulation failure.
Peak Factor of Various AC Waveforms
| Waveform | Waveshape | PF |
| Sinusoidal |  | 1.414 |
| Triangular | 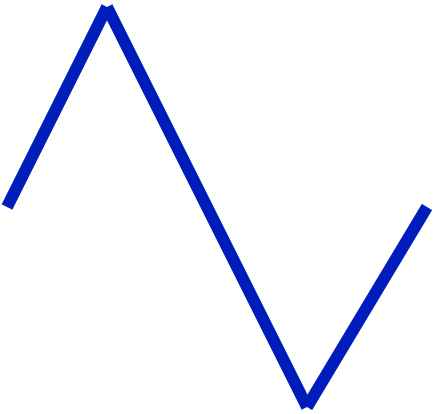 | 1.732 |
| Squre |  | 1 |
| Sawtooth |  | 1.732 |
Numerical Example
Q. 1 The RMS value and maximum value of a sinusoidal voltage are 282.5 and 400 volts, respectively. Calculate peak factor.
Given Data:
Vrms = 282.5 V
Vm = 400 V
PF=?

The peak factor is 1.414.
Q. 2 The RMS value and maximum value of a sinusoidal voltage are 300 and 500 volts, respectively. Calculate its crest factor.
Given data-
Vrms = 282.5 V
Vm = 400 V
PF=?

Peak Factor 1.66 shows that the sinusoidal wave is distorted.