The k-factor of the transformer is a weighting of the harmonic load currents based on their effects on transformer heating, derived from ANSI/IEEE C57.110.
Transformers are fundamental components in electrical systems, playing a crucial role in voltage regulation and power distribution. However, standard transformers can face operational challenges in systems with non-linear loads due to the harmonic currents produced by these loads. The K factor of a transformer is a critical measure that helps in assessing and addressing these challenges. This article explores the concept of the K factor in transformers, how it affects transformer ratings, and the mathematical formula used to calculate it.
What is the K Factor of a Transformer?
The K factor is a numerical indicator used to quantify the ability of a transformer to handle the effects of harmonic currents generated by non-linear loads without incurring significant damage or reduction in efficiency. Non-linear loads, such as variable frequency drives, UPS systems, and computers, draw current in abrupt pulses rather than as a smooth sinusoidal wave, resulting in the generation of harmonics that can cause heating and other detrimental effects in power distribution systems.
Importance of K Factor of Transformer
The significance of the K factor in transformers arises from its direct impact on the lifespan and efficiency of these devices under the stress of harmonic currents. A transformer with a higher K factor rating is better equipped to handle the extra heat and other stresses induced by harmonics, thus ensuring more reliable operation and longevity when serving non-linear loads. This factor is particularly crucial in industrial and commercial settings where electronic equipment generating harmonic loads is prevalent.
Rating Calculation for Transformers with K Factor
The rating of a transformer concerning its K factor involves determining how much harmonic current the transformer can handle safely compared to a standard transformer without a specified K factor. The calculation assesses the transformer’s ability to endure the additional heating effect caused by harmonic frequencies. The standard formula to calculate the K factor is:
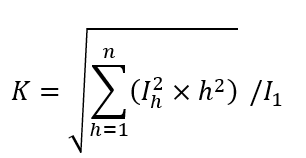
Where:
- K is the K factor of the transformer.
- Ih represents the RMS current of the hth harmonic.
- h is the harmonic order (i.e., 1st harmonic is the fundamental frequency, 2nd is double the fundamental frequency, etc.).
- I1 is the RMS current at the fundamental frequency.
- n is the number of harmonics considered in the calculation.
Formula Explanation
The formula for K factor takes into account the square of the harmonic order multiplied by the square of the RMS current for each harmonic, summing up these values for all significant harmonics present in the system. This sum is then divided by the square of the RMS current at the fundamental frequency. The square root of the resultant value gives the K factor, which effectively weights the transformer’s tolerance to higher-order harmonics more heavily, reflecting their greater potential for causing damage.
Solved Problems on K-Factor of Transformer
To illustrate how the K factor of a transformer is calculated and applied, let’s go through a couple of solved example problems. These examples will help clarify the use of the K factor formula and its significance in selecting transformers suitable for handling non-linear loads with harmonic distortions.
Problem 1: Calculating the K Factor
Given: A transformer supplies a load that draws a fundamental frequency current (I1) of 100 amps and harmonic currents as follows:
- 2nd harmonic: 30 amps
- 3rd harmonic: 40 amps
- 5th harmonic: 20 amps
- 7th harmonic: 10 amps
Calculate the K factor for this transformer.
Solution:
- Identify the RMS currents and their corresponding harmonic orders:
-
- I1=100 AIfundamental frequency)
- I2=30A (2nd harmonic)
- I3=40A (3rd harmonic)
- I5=20A (5th harmonic)
- I7=10A (7th harmonic)
- Apply the K factor formula:

Conclusion: The K factor for this transformer is approximately 1.84, which indicates a moderate level of harmonic handling capability. This transformer is suitable for applications with relatively low harmonic content.
Problem 2: Transformer Selection Based on K Factor
Given: An industrial site requires a transformer to handle the following harmonic load:
- Fundamental frequency current: 150 amps
- Total harmonic distortion (THD): 35%
Objective: Select a suitable transformer
Solution:
- Estimate the effective harmonic current using THD:
- THD is defined as the ratio of the total harmonics’ RMS current to the fundamental RMS current.
- Using THD to estimate the effective harmonic current:
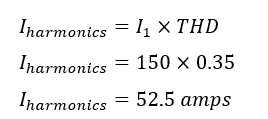
2. Assume a simplified case with major harmonics (e.g., 3rd, 5th) contributing to the THD:
- For simplicity, let’s assign 30 amps to the 3rd harmonic and 22.5 amps to the 5th harmonic.
3. Recalculate the K factor with estimated values (simplified):
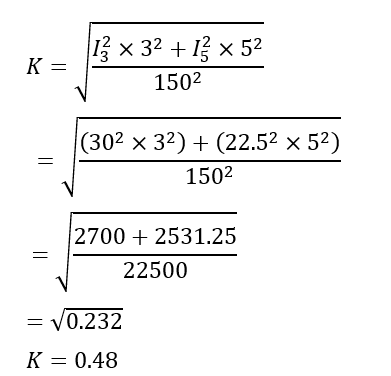
Conclusion: For an accurate selection, the industrial site should use a transformer with a K factor rating higher than the calculated value, ideally a transformer with a K factor of 1 or higher to ensure safe operation under harmonic loads.
Practical Application and Transformer Selection
When selecting a transformer for a system with a significant presence of non-linear loads, it is essential to choose a transformer with an appropriate K factor rating. A transformer with a K factor of 1 is suitable for linear loads only, whereas transformers with higher K factors are designed to handle increasing levels of harmonic currents. Typical industry standards provide K factors such as 4, 9, 13, etc., each suitable for different levels of harmonic distortion.
Conclusion
The K factor of a transformer is a pivotal metric in the design and selection of transformers intended for environments with non-linear loads. Understanding and applying the K factor ensures that transformers are adequately equipped to handle the adverse effects of harmonic currents, thereby enhancing system reliability and efficiency. As electronic devices proliferate and become increasingly complex, the relevance of the K factor in transformer technology continues to grow, guiding the development of more robust and harmonic-resistant transformers.