Alternating current (AC) constantly changes direction, making direct measurement of its power challenging. The effective value of alternating current (RMS) provides a practical way to express AC in terms of its equivalent DC effect, helping engineers and students calculate power, design circuits, and analyze electrical systems accurately.
Definition of Effective Value of Alternating Current (RMS)
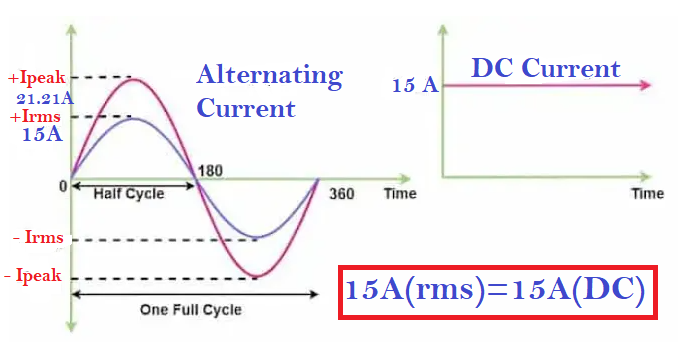
The effective value of alternating current is equal to the value of the steady current (DC Current), which, when passed through a resistor for a specified time, produces the same amount of heat that an alternating current when passed through the same resistor for the same time. The effective or RMS value of alternating current is also called the RMS value.
Let us understand this definition with an example.
Suppose 15 ampere AC RMS or effective current passes through a resistor that has 10 ohms resistance. Then, the heat produced in the resistor is;
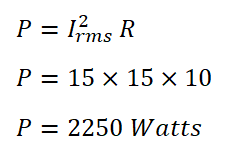
Now, if the steady current passes through the same resistor for the same time, what is the current’s magnitude that can produce the 2250 watts?
As per the definition, the 15 ampere DC current or steady current will produce the same amount of heat. Thus, if 15 ampere DC current flows through the 10 ohms resistor, it will produce the same amount of heat, i.e., 2250 watts.
The effective value or RMS value of alternating current is shown in the image below.
Importance of Effective Value of AC
The RMS or effective value is important because:
- It allows AC circuits to be compared to DC circuits in terms of heat production.
- It helps in practical calculations for power and energy in AC devices.
- RMS value ensures compatibility with resistive loads, making AC measurement meaningful.
Methods of Calculation of RMS Value
There are two methods that can be used to calculate the RMS value.
- Graphical method
- Analytical Method
Graphical Method
In the graphical method, we calculate the RMS value as the square root of the mean of the squares of the current.
Analytical Method
In the analytical method, we use formulas to calculate RMS values depending on the type of waveform (sinusoidal, triangular, etc.)
Formulas for Effective (RMS) Current
Graphical Method:
RMS value = square 𝐫𝐨𝐨𝐭 of 𝐦𝐞𝐚𝐧 of the 𝐬𝐪𝐮𝐚𝐫𝐞𝐬 of the current

Analytical Method:
Formulas vary depending on waveform:
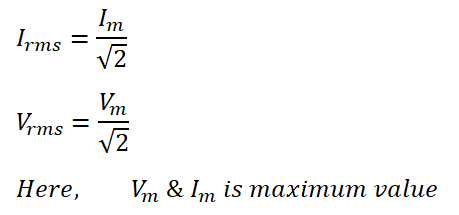
For Derivation of Formulas, you may read– Derivation of RMS value of AC current.
Numerical Examples of Effective Current
Example 1 – A sinusoidal current has a maximum value of 10 amperes. What is its RMS value?
Solution:

Example 2 – The equation of alternating voltage is i = 400 𝑠𝑖𝑛314𝑡. Calculate RMS value
Solution:
The maximum value of the current is 400 volts.
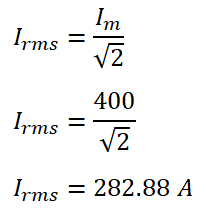
Conclusion
The effective value of alternating current (RMS) represents the DC equivalent of an AC current in terms of heat production. Understanding RMS helps in accurate calculation and analysis of AC circuits. Using formulas and examples, the effective value ensures practical and precise electrical measurements.
Related Articles: