This article describes two important transformer ratios: turn ratio and voltage transformation ratio. Transformers are fundamental components in electrical engineering, playing a crucial role in transmitting, distributing, and utilizing electrical power. Their ability to efficiently change voltage levels is pivotal in ensuring electricity’s safe and economical distribution over long distances. Central to understanding a transformer’s operation is the Turns Ratio and Voltage Transformation Ratio. These ratios not only define a transformer’s basic functionality but also provide insights into its design and application in electrical systems.
Turns Ratio of Transformer
The Turns Ratio of a transformer is a fundamental aspect that determines its ability to convert one voltage level to another. It is the ratio of the number of turns in the primary winding (N₁) to the number of turns in the secondary winding (N₂). Mathematically, it is expressed as:
Turns Ratio=N1 /N2
We can also write the transformer’s turn ratio in terms of primary and secondary voltage.
Turns Ratio=N1 /N2=V1 / V2
This ratio is a critical design parameter directly influencing the transformer’s voltage transformation characteristics. If the primary winding has more turns than the secondary winding, the transformer reduces voltage and increases current, functioning as a step-down transformer. Conversely, if the secondary winding has more turns, the transformer increases voltage and decreases current, operating as a step-up transformer.
Voltage Transformation Ratio of Transformer
While the Turns Ratio provides a theoretical framework, the Voltage Transformation Ratio (VTR) offers a practical perspective. It represents the ratio of the transformer’s secondary voltage (V₂) to its primary voltage (V₁), under the condition of no load to minimal load. It can be represented as:
Voltage Transformation Ratio (VTR)=V2 /V1
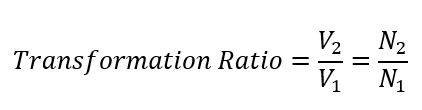
Ideally, the VTR is directly proportional to the Turns Ratio, assuming perfect efficiency and no losses. However, in real-world applications, transformers exhibit inherent inefficiencies due to factors like resistance in windings, magnetic hysteresis, and eddy current losses, which slightly alter the practical VTR from the theoretical Turns Ratio.

Implications and Applications of Turn Ratio & Voltage Transformation Ratio
Understanding and controlling the Turns Ratio and VTR is crucial for designing and operating transformers in electrical systems. For instance, step-down transformers are used in power distribution systems to decrease the voltage from high transmission levels to safer levels suitable for domestic or industrial use. Similarly, step-up transformers are employed at generation sites to increase voltage levels, minimizing energy loss over long-distance transmission.
Moreover, the precision in maintaining a specific Turns Ratio and VTR is essential for applications requiring high accuracy, such as instrumentation transformers used in measurement and protective devices. Any deviation in these ratios can lead to significant measurement errors or system malfunctions.
Solved Examples:
Let’s discuss numerical examples that illustrate the concepts of Turns Ratio and Voltage Transformation Ratio in transformers to provide a clearer understanding of these principles in action.
Example 1: Calculating Turns Ratio
Given: A step-down transformer designed to convert a primary voltage of 240V to a secondary voltage of 120V. The primary winding has 480 turns.
Find: The number of turns in the secondary winding and the Turns Ratio.
Solution:
The Voltage Transformation Ratio (VTR) can be found using the formula:
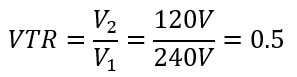
Since the Turns Ratio (TR) is directly proportional to the VTR in an ideal transformer, we can write:
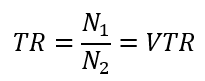
Given that N1=480 turns, we can rearrange the formula to solve for N2:
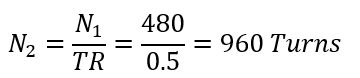
This result implies a mistake in our calculation, as we expected a step-down transformer (which should reduce voltage and, accordingly, should have fewer turns on the secondary). Let’s correct the calculation:
The correct approach should consider that the TR for a step-down transformer would actually be the inverse of the VTR, meaning:
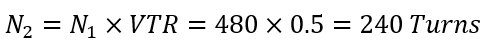
The secondary winding should have 240 turns, making the Turns Ratio 480/240=2
Example 2: Determining Output Voltage Using Turns Ratio
Given: A step-up transformer has 100 turns on the primary winding and 500 turns on the secondary. If the primary voltage is 110V, what is the secondary voltage?
Find: The secondary voltage.
Solution:
First, determine the Turns Ratio:
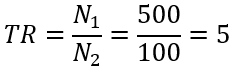
Then, apply the TR to find the secondary voltage:
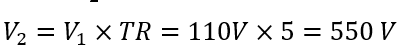
The secondary voltage of this step-up transformer would be 550V.
Conclusion
The Turns Ratio and Voltage Transformation Ratio are key concepts in transformer operation and understanding. They dictate the transformer’s basic functionality and have profound implications on its efficiency, application, and design. By carefully designing and maintaining these ratios, engineers can optimize transformers for various applications, ensuring efficient, reliable, and safe electrical power distribution and utilization.