Millman’s Theorem: Statement, Formula, Proof, and Solved Problems

Millman Theorem is a powerful concept in electrical engineering that simplifies the analysis of complex circuits. It is widely used for solving parallel branches with voltage or current sources. In this article, we will cover Millman’s Theorem statement, formula, proof, solved problems, applications, and limitations to give you a complete understanding.

What is Millman’s Theorem?

Millman’s Theorem is a technique used in electrical circuit analysis to determine the voltage across parallel branches without complex calculations. It allows engineers to find the equivalent voltage for multiple branches connected in parallel.

In simpler terms, instead of solving several loops individually, Millman’s Theorem provides a shortcut to find the voltage directly.

Millman’s Theorem Statement

The statement of Millman’s Theorem is:

For a network of n parallel branches, each containing a voltage source and series resistance, the voltage across the parallel combination can be calculated using the sum of the branch voltages divided by the sum of branch conductances.

Millman Theorem Formula

Millman’s Theorem formula can be expressed in two cases:

1. For Voltage Sources in Parallel with Series Resistances:

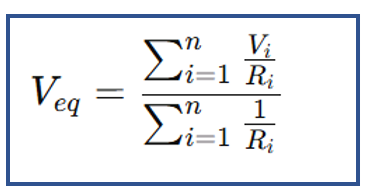
Where:

• V_eq = voltage across the parallel combination
• V_i= voltage of the ith branch
• R_i = series resistance in the ith branch

This formula is also referred to as the Millman Formula.

2. For Mixed Voltage and Current Sources in Parallel:

Where Ii is the current of each parallel branch.

Millman’s Theorem Proof

The proof of Millman’s Theorem is derived from Kirchhoff’s Current Law (KCL):

Step 1: Consider the Circuit

• Let n branches are connected in parallel.
• Each branch has a voltage source V_i​ and a series resistance R_i​.
• Let the voltage across the parallel combination be V_eq​.

Step 2: Current Through Each Branch

The current through the i-th branch is:

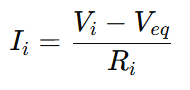
Step 3: Apply Kirchhoff’s Current Law (KCL)

Step 4: Solve for V_eq

Rearranging the equation:

This proves the Millman Formula for voltage across parallel branches.

Solved Problems Using Millman Theorem

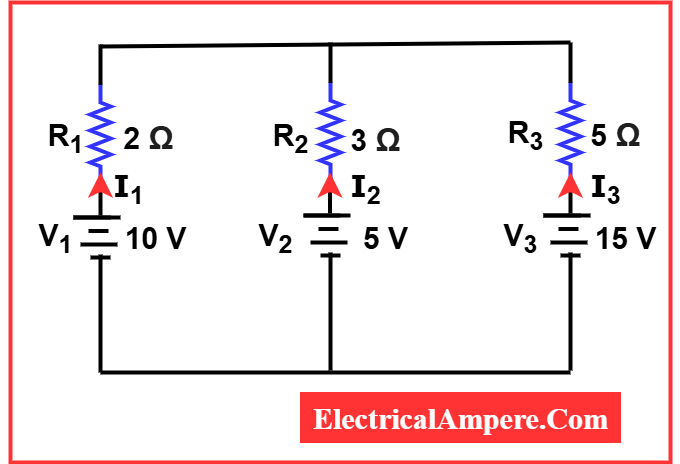
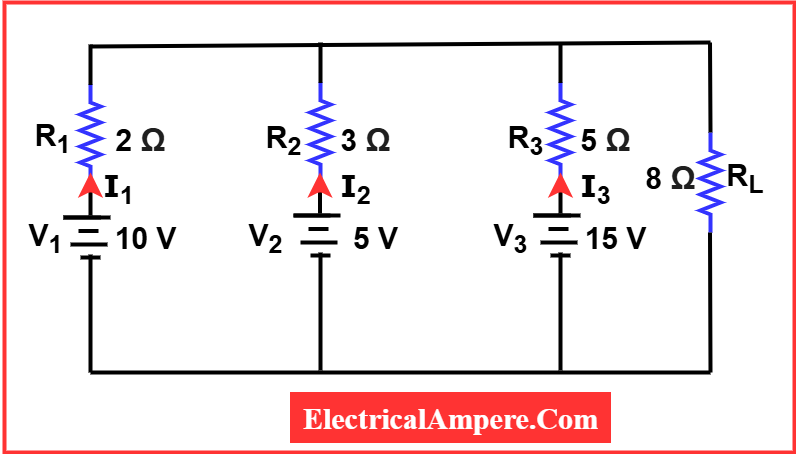
Problem 1: Three voltage sources are connected in parallel with series resistances:

• V₁=10V,R₁=2Ω
• V₂=5V,R₂=3Ω
• V₃=15V,R₃=5Ω

Find current in each branch.

Solution:

Step 1: Calculate Equivalent Voltage (Thevenin voltage) V_eq

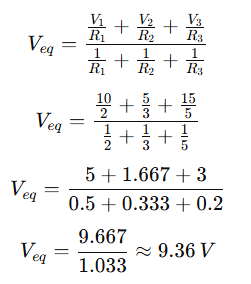
Step 2: Calculate Current in Each Branch

Current through each branch is:

Branch 1:

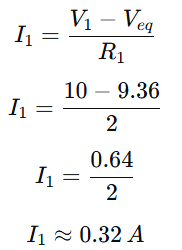
Branch 2:

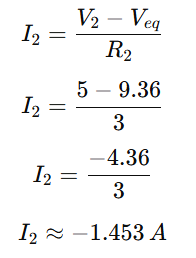
Negative current in Branch 2 indicates current is flowing opposite to the assumed direction.

Branch 3:

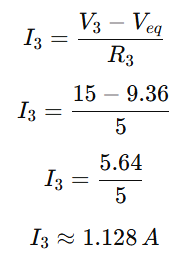
Problem 2: Calculate the voltage across the 8 Ω load, which is connected across the series combination of voltage source V3 and resistor R3​, as shown in the circuit below.

As calcullated in example-1, the equivalent voltage of aall voltage sources.

V_eq= 9.36 Volts

The equivalent resistance of the circuit,

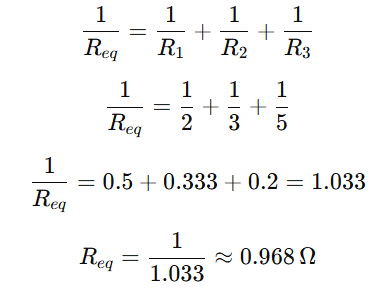
Now, we can represent the above circuit as its equivalent circuit.

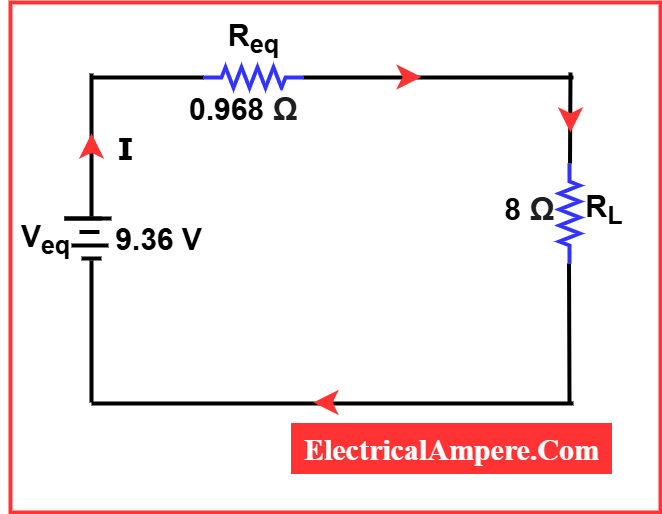
Current though 8Ω load resistor,

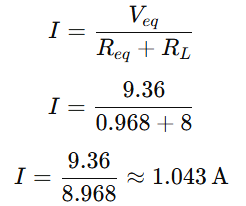
Let’s calculate the voltage across the load:

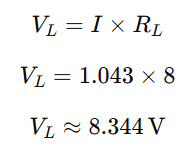
Millman’s Theorem for Circuits with Mixed Sources

Millman’s Theorem is not only useful for parallel voltage sources but can also simplify circuits containing a combination of voltage and current sources connected in parallel. By applying this theorem, the network can be reduced to a single equivalent voltage or current source, making analysis much simpler.

Circuit Representation

Consider a circuit with multiple voltage and current sources in parallel (as shown in Figure F). Each source follows conventional notation.

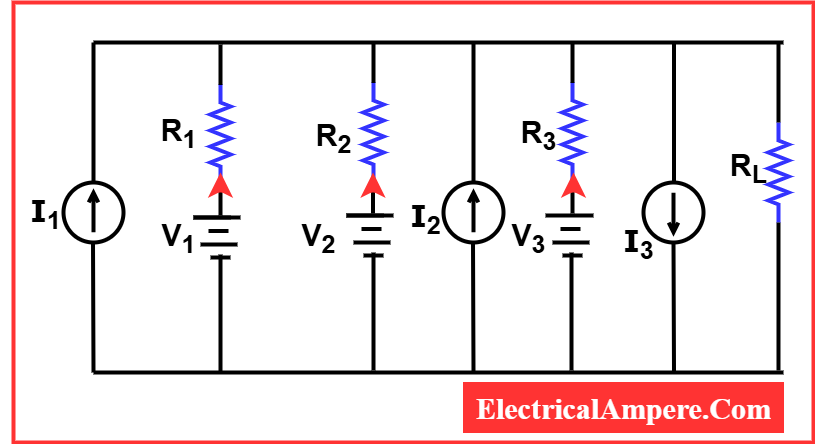
• V_eq: The equivalent voltage (Thevenin voltage) calculated using Millman’s Theorem.
• R_eq: The equivalent resistance (Thevenin resistance), obtained by replacing all current sources with open circuits and voltage sources with short circuits.

Millman’s Theorem reduces this complex circuit to a simpler form, as shown in the figure below.

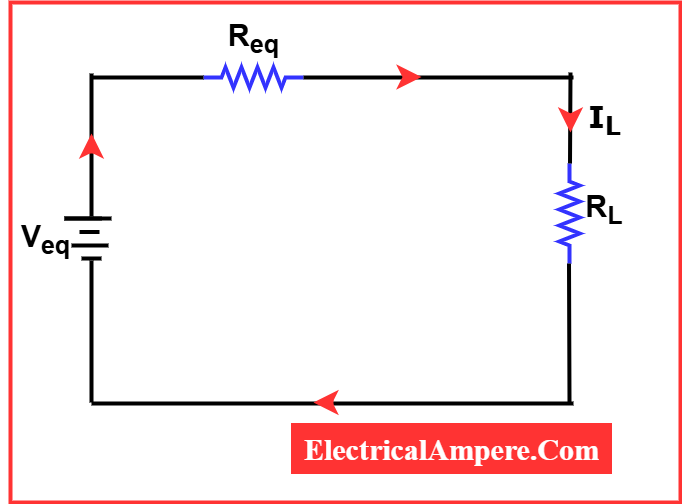
Calculating Load Current and Terminal Voltage

Once the circuit is simplified, it becomes straightforward to determine:

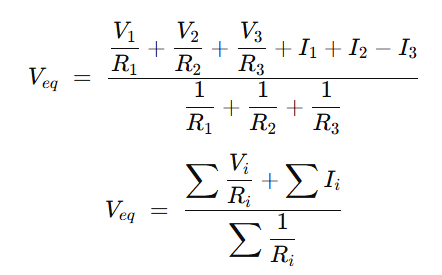
We determine the Thevenin resistance (R_eq) by replacing all current sources with open circuits and all voltage sources with short circuits.

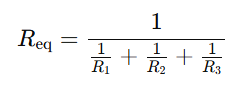
We can now easily calculate the load current I_L​ and the terminal voltage V_T using Ohm’s law.

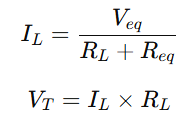
To illustrate this process, let’s consider a practical example with a mixed-source parallel circuit. Millman’s Theorem quickly gives the equivalent voltage and resistance, enabling direct calculation of load current and terminal voltage

Eaxmple on Millman’s Theorem for Circuits with Mixed Sources

Example: Using Millman’s theorem, find the current through the 8 Ω load resistor in the mixed voltage and current sources circuit shown below.

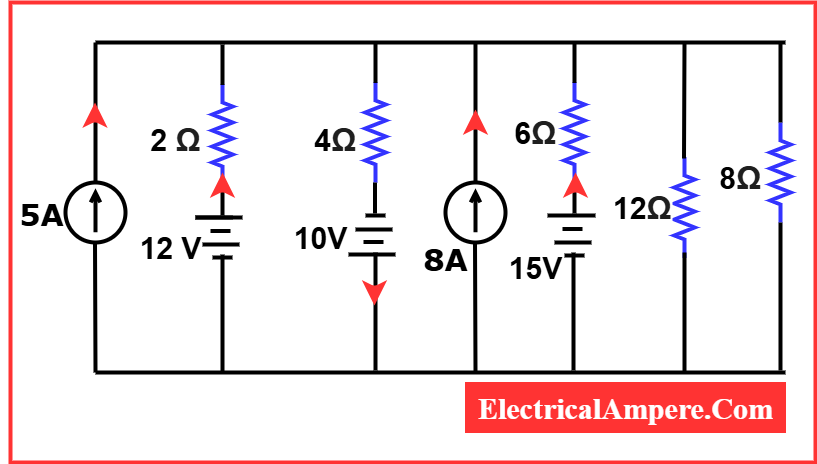
Let us first find thevenin equivaalent voltage V_eq,

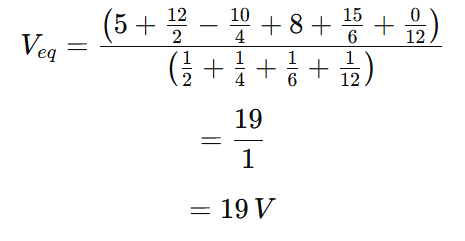
Thevenin equivalent resistance R_th;

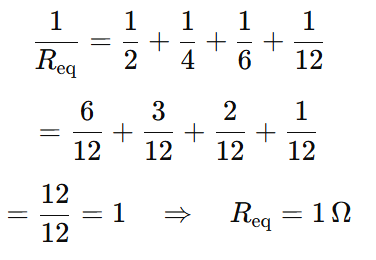
Now, we can draw the equivalent circuit using the V_eq​ and R_th values.

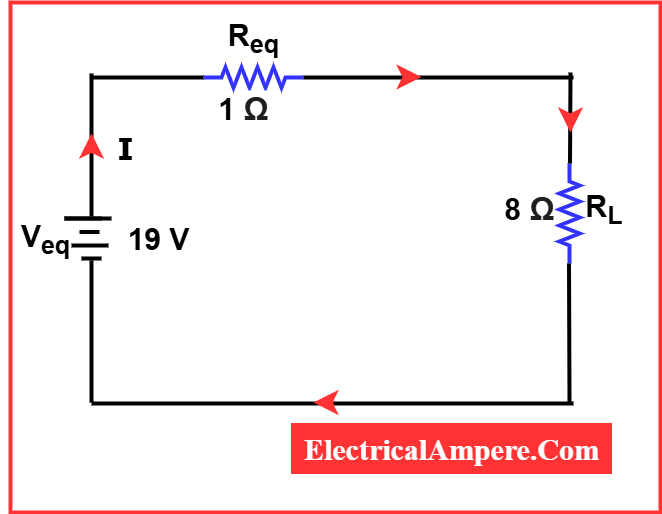
The current through 8 Ω load resistor is:

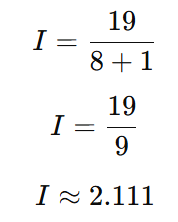
Current through the 8 Ω load resistor is 2.111 Amperes.

Applications of Millman Theorem

Millman’s Theorem is applicable in:

• Simplifying parallel resistor networks with voltage sources
• Analyzing complex electrical circuits in electronics
• Calculating node voltages in power systems
• Designing analog circuits

It yields equivalent voltage or equivalent current, making it extremely useful for engineers.

Limitations of Millman’s Theorem

While useful, Millman’s Theorem has some limitations:

• Only applicable for parallel branches
• Not suitable for series circuits
• Cannot handle dependent sources directly without modifications
• Less effective for highly complex networks with multiple loops

Conclusion

Millman’s Theorem simplifies the analysis of parallel electrical circuits with voltage and current sources. Using the Millman formula, engineers can quickly calculate the equivalent voltage across branches without lengthy calculations.

For anyone preparing for electrical engineering exams or working on circuit analysis, mastering Millman’s Theorem and practicing problems with solutions is essential.

Related Articles:

1. Superposition Theorem
2. Maximum Power Transfer Theorem
3. Reciprocity Theorem