Faraday’s Induction Law explains electromagnetic induction—how changing magnetic fields generate EMF to power generators, transformers, and modern devices. In this article, we’ll explore Faraday’s 1st law, Faraday’s 2nd law, its mathematical expression, practical applications, and experimental observations.
What is Faraday’s Induction Law?
Faraday’s Induction Law explains how a changing magnetic field can induce an electromotive force (EMF) or voltage in a conductor. This phenomenon is called electromagnetic induction.
Definition: Law of Electromagnetic Induction
When a magnetic field around a conductor changes, it induces an electromotive force (EMF) in the conductor.
This simple yet powerful law explains how mechanical energy is converted into electrical energy in generators.
Faraday’s Laws Explained: First & Second
The laws of Faraday are divided into two parts: Faraday’s First Law and Faraday’s Second Law. Let’s understand each.
First Law Explained
Faraday’s First Law states:
Whenever the magnetic flux linked with a coil changes, an EMF is induced in the coil. If the circuit is closed, the current flows.
In simpler terms:
- EMF is induced only when there is a change in magnetic field.
- No change = No EMF.
Faraday’s Experiment: In his classic setup, Faraday moved a magnet through a coil and observed the generation of current in a galvanometer. See detailed diagram.
Second Law Explained: Flux-Change Principle
Faraday’s 2nd law of electromagnetic induction quantifies the EMF induced:
The magnitude of EMF is directly proportional to the rate of change of magnetic flux linkage.
Faraday’s Law Formula: EMF Expression
The induced EMF in a coil due to changing magnetic flux is given by:
EMF (E) = – N × (dΦ / dt)
Where:
- E = Induced EMF
- N = Number of turns in the coil
- Φ = Magnetic flux (in Weber)
- dΦ/dt = Rate of change of flux
- The negative sign is due to Lenz’s Law, indicating opposition to the change.
This formula clearly establishes the magnetic flux and EMF relationship, where the rate of flux change determines the magnitude of the induced EMF.
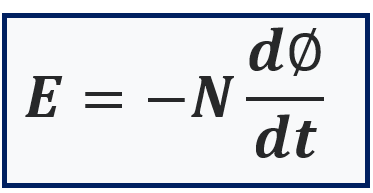
Derivation of Faraday’s Induction Law
Consider a magnet approaching a coil. Let the magnetic flux linkage with the coil at time T1 be NΦ1, and at time T2 be NΦ2. The change in flux linkage over this time interval is:

Let the change in magnetic flux be denoted as:
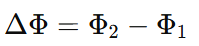
Then the total change in flux linkage becomes:
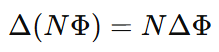
If this change occurs over a time interval t, the rate of change of flux linkage is:
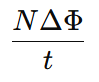
For instantaneous change, taking the derivative with respect to time gives:
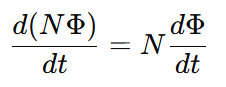
According to Faraday’s second law of electromagnetic induction, the induced electromotive force (EMF) in the coil is equal to the rate of change of magnetic flux linkage. Therefore:

This derivation highlights the direct relationship between flux linkage and EMF, forming the basis of how voltage is induced in a coil when the magnetic environment changes.
Now, considering Lenz’s Law, which states that the induced EMF always opposes the change in magnetic flux that caused it, we introduce a negative sign:
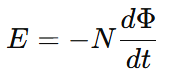
From this equation, we can draw the following conclusions:
- Increasing the number of turns in the coil (N) increases the induced EMF(E).
- Increasing the magnetic field strength increases the rate of flux change (dΦ/dt)), thus increasing EMF.
- Increasing the relative speed between the magnet and the coil also increases the induced EMF.
Core Concepts of Electromagnetic Induction
| Concept | Explanation |
|---|---|
| Faraday’s Law of Induction Formula | Shows EMF is proportional to flux change |
| Induction Law | Basis of voltage generation in coils |
| Faraday Principle | Magnetic field variations create electric fields |
| Faraday’s Law Electromagnetic Induction | Unifies magnetism and electricity in practical systems |
| Faraday’s Law Diagram | Typically shows a magnet, coil, and galvanometer |
Faraday’s Experiment with Magnet and Coil (Diagram Analysis)
The diagram below demonstrates how Faraday’s Law works using a simple magnet-and-coil setup:
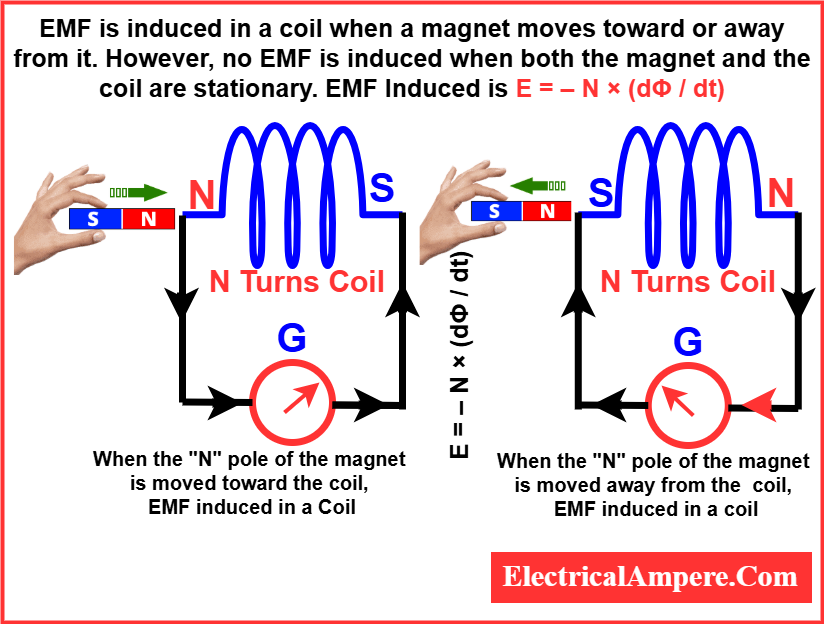
When a magnet moves toward the coil, the magnetic flux through the coil increases, leading to EMF generation in the coil due to flux change, as explained by Faraday’s Law of Electromagnetic Induction.
When the magnet moves away, the magnetic flux decreases, inducing an EMF in the opposite direction. If the magnet is stationary and the coil is moving, a similar change in magnetic flux occurs, and EMF is still induced. However, if both the magnet and coil are stationary, there is no change in magnetic flux, and no EMF is induced.
| Condition | Deflection in Galvanometer / EMF Induction |
|---|---|
| Magnet and coil both at rest | No deflection in the galvanometer (No EMF induced) |
| Magnet moves toward the coil | Deflection in the galvanometer in one direction (EMF induced) |
| Magnet is held stationary near the coil | No deflection in the galvanometer (No EMF induced) |
| Magnet moves away from the coil | Deflection in the galvanometer in the opposite direction (EMF induced) |
| Coil moves toward or away from a stationary magnet | Deflection in the galvanometer (EMF induced) |
| Magnet held stationary far from the coil | No deflection in the galvanometer (No EMF induced) |
This demonstrates that it is the relative motion between the coil and the magnetic field that causes electromagnetic induction.
Applications of Electromagnetic Induction in Real Life
The Faraday Induction Law is widely used in:
- Electric Generators – Converts mechanical energy to electrical energy
- Transformers – Transfer energy between circuits via electromagnetic induction
- Induction Cooktops – Use magnetic fields to heat vessels
- Electric Guitars – Use pickup coils based on Faraday’s Law
- Wireless Charging – Uses alternating magnetic fields to induce EMF
These examples illustrate the relevance of Faraday’s law in real life applications across industries.
Importance of Faraday’s Induction Law in Modern Technology
Understanding the law of Faraday is critical because:
- It explains how electricity can be generated from motion
- It laid the foundation for electric power generation and distribution
- It supports key principles of modern electromagnetism
- This principle of EMF generation in coil forms the foundation of modern electric power generation systems.
Conclusion: Why Faraday’s Law Still Matters Today
Faraday’s Induction Law is a fundamental principle that links magnetism and electricity. It explains how changing magnetic fields can induce current in conductors—a discovery that revolutionized technology. From electric motors to transformers, Faraday’s Law of Electromagnetic Induction is at the heart of our modern electrical world.
The applications of electromagnetic induction extend from everyday appliances like induction cooktops to advanced industrial systems such as power generators, wireless charging, and medical imaging.
Whether you’re studying physics or working on an engineering project, a strong understanding of the Faraday electromagnetic induction law is essential.
FAQs on Faraday’s Induction Law
EMF(E)=−NdΦ/dt
It is the total magnetic field passing through a surface area of a coil.
No. Lenz’s Law explains the direction of induced EMF, while Faraday’s Law gives its magnitude.
First Law:
EMF is induced in a conductor when the magnetic flux linked with it changes.
Second Law:
The induced EMF is proportional to the rate of change of magnetic flux linkage.
Formula:
E = –N × (dΦ/dt)
These laws explain how changing magnetic fields produce electricity in devices like generators and transformers.
The induced EMF depends on:
Number of turns (N) in the coil
Rate of change of magnetic flux (dΦ/dt)
Strength of the magnetic field
Relative speed between the coil and the magnetic field
Angle between the magnetic field and the coil surface
Greater any of these factors, stronger the induced EMF. The magnetic flux and EMF relationship is core to understanding how quickly changing fields can induce stronger voltages.
References
Related Articles: