Definition: The RMS value of an alternating current(AC) is equal to the value of a steady current (DC Current) that produces the same amount of heat as the alternating current when passed through a resistor for the same amount of time. Therefore, the RMS value of an alternating current is the value of the steady current that would produce the same amount of heat as the alternating current. The abbreviation RMS stands for Root-Mean-Square of instantaneous current values.
Mathematically, for an AC waveform v(t) over one period T, the RMS value Vrms is calculated as follows:
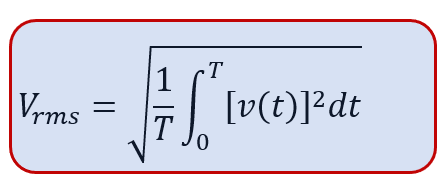
The formula for Irms is;

In simpler terms, the RMS value of alternating current is the square root of the average of the squared values of the instantaneous voltage or current over one complete cycle. It represents the equivalent steady DC value that produces the same amount of power dissipation or heat in a resistive load as the AC waveform
RMS Value of AC
You can determine the RMS value of alternating current by the direct current flowing through a resistance. It’s important to note that the RMS value of AC is higher than its average value. To determine the RMS value of a sine current wave, you need to calculate the area covered in a half-cycle. This method is applicable to all kinds of waves, whether they’re sinusoidal, non-sinusoidal, symmetrical, or asymmetrical. Irms or Iv denotes the RMS value. This is the graphical method of determining RMS value. The other method is the analytical method for determining the RMS value of AC.
We will derive the RMS formula using an analytical method.
RMS Value of AC Formula
The following formula expresses the formula of the RMS value( Irms and Vrms) of alternating current.

RMS Value of AC Derivation
To calculate the RMS value of alternating current, we need to determine the heat generated during one half-cycle of the waveform.
The alternating current flowing in a resistor(R) produces heat in the resistor. The circuit diagram is shown below,
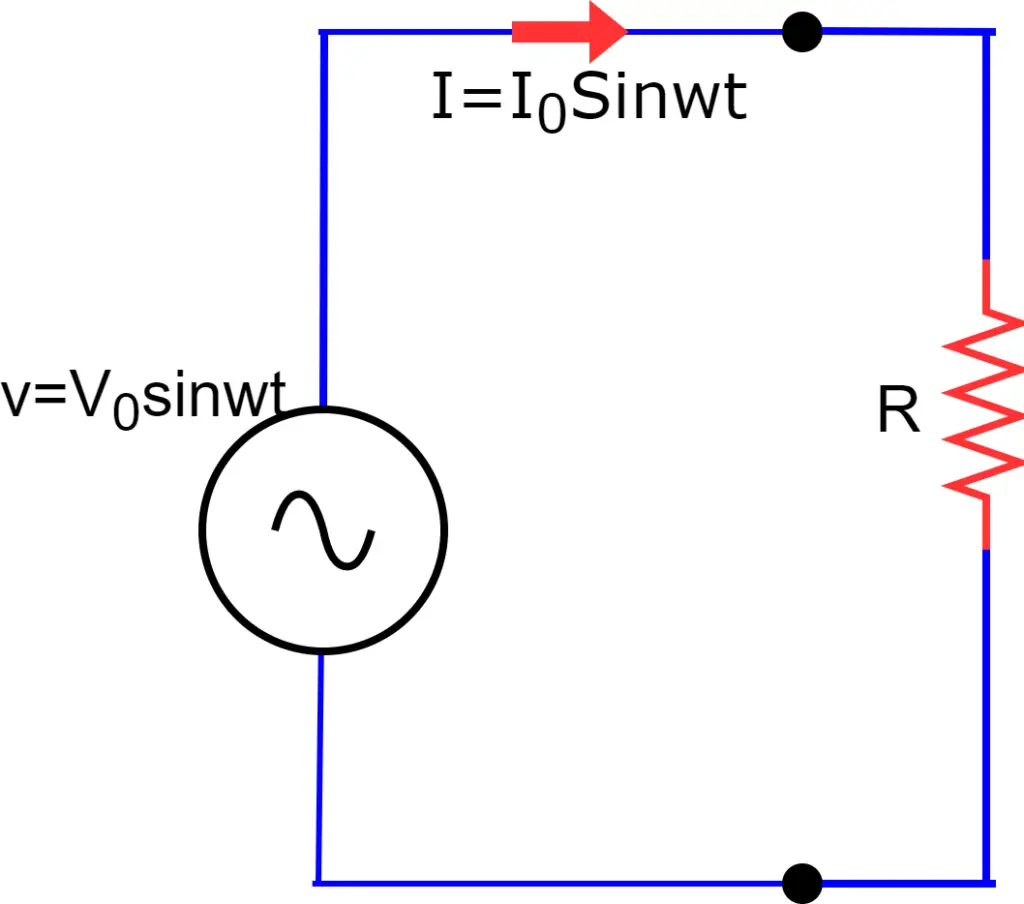
The current flowing in the circuit is I0sinwt, producing heat(H) in the resistor(R).
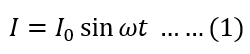
The heat produced by current in t time is;

Heat produced in dt time is d(H),

Putting the value of current(I) from equation 1 in equation 2, we get;
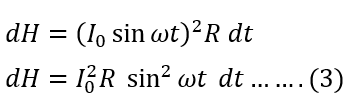
The heat produced in T/2 time is;
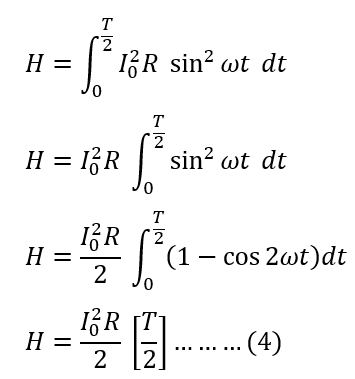
The RMS value of AC is represented as:

Equating equations 4 and 5, we get the RMS value of alternating current;
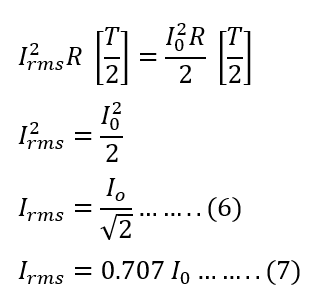
Solved Example
Q.1 The peak value of sinusoidal voltage is 615 volts. Calculate the RMS voltage of AC.

Q.2 The current flowing in a circuit is i=15 sin314t. Calculate the RMS value of the alternating current.
Given Date-
I0= 15 amperes

Conclusion
In conclusion, the RMS (Root Mean Square) value of an Alternating Current (AC) waveform is a crucial parameter that represents the effective or equivalent value of the AC signal. The RMS value simplifies calculations in AC circuits by providing an equivalent DC value that would produce the same heating effect in a resistive component.
For a sinusoidal AC waveform, you can calculate the RMS value by taking the square root of the mean of the squared instantaneous values over one complete cycle.