Definition: The coefficient of coupling, denoted by (k), represents the proportion of magnetic flux generated by the current in one coil that interlinks with the other coil. It is also known as the coupling factor.
Coefficient of Coupling Between Two Coils
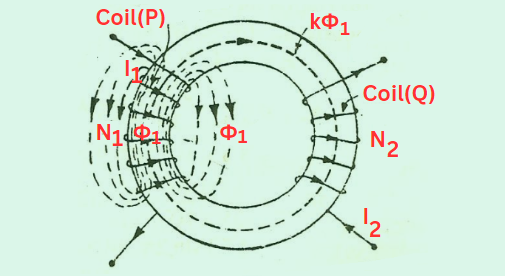
Consider two coils, P and Q. When current flows through coil P, it generates magnetic flux that links with coil Q. However, not all of the flux produced by coil P may or may not be linked entirely with coil Q.
Similarly when current passes through coil Q, it generates flux, which may or may not be entirely linked with coil P. This incomplete linking happens due to the flux leakage, represented by a fraction (k) known as the Coefficient of Coupling(k).
Case 1: k = 1: Magnetically Tightly Coupled Coils
When k=1, it indicates that the flux generated by one coil fully links with the other coil, resulting in a state known as magnetically tightly coupled.
Case 2: k = 0: Magnetically Isolated Coils
On the other hand, when k=0, it signifies that the flux from one coil doesn’t link with the other, indicating that the coils are magnetically isolated.
Coefficient of Coupling Formula
The coefficient of coupling (k) can be calculated using the relationship between mutual inductance (M) and self-inductances (L1 and L2) of the two coils:
Where:
- k = Coefficient of Coupling
- M = Mutual Inductance of the two coils
- L1 = Self-Inductance of coil 1
- L2 = Self-Inductance of coil 2
Coefficient of Coupling Formula Derivation
Consider two magnetic coils, P and Q. (As shown in Fig.-1)
Step 1: Current Through Coil P
When current I1 flows through coil P, The self-inductance (L1) and mutual inductance(M) of the coil is :
Step 2: Current Through Coil Q
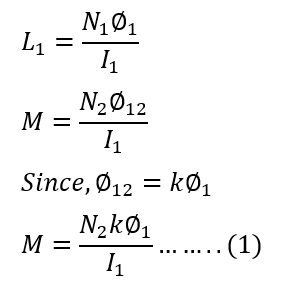
When current I2 flows through coil Q, The self-inductance (L2) and mutual inductance(M) of the coil is :
Step 3: Calculating the Coefficient of Coupling
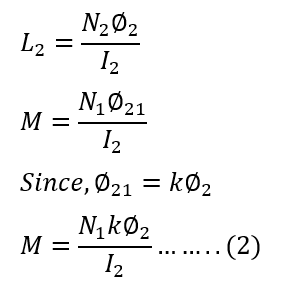
By multiplying equations 2 and 3, we can calculate the coupling factor.
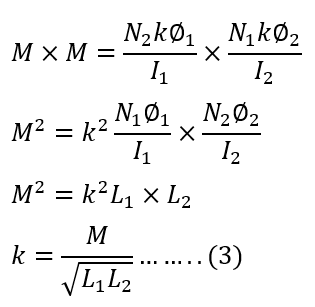
Equation (3) above illustrates the relationship between the mutual inductance and self-inductance of the two coils.
Solved Example on Coefficient of Coupling
The self-inductance of the two coils is 75 and 120 mH, respectively. The mutual inductance of the coils is 50 mH. Calculate the coupling factor (k).
Conclusion
The coefficient of coupling (k) indicates how efficiently magnetic flux links between two coils, ranging from 0 (magnetically isolated) to 1 (magnetically tightly coupled). By knowing the mutual inductance (M) and self-inductances (L1 and L2), it can be calculated using the formula k = M / √(L1 × L2). Understanding this parameter is essential for designing efficient transformers, inductors, and other magnetic devices.
Related Articles: